Suppose That the Function F a b r is Uniformly Continuous Prove That F a b r is Bounded

This topic concerns a very classical question: extend of a function $f : X \to Y$ between two metric spaces to obtain a new function $\widetilde f : \overline X \to Y$ enjoying certain properties . I am interested in the following three properties:

Continuity,
Uniformly continuity,
Pointwise equi-continuity, and
Uniformly equi-continuity.

Throughout this topic, by $X$ and $Y$ we mean metric spaces with metrics $d_X$ and $d_Y$ respectively.

CONTINUITY IS NOT ENOUGH . Let us consider the first situation where the given function $f : X \to Y$ is only assumed to be continuous. In this scenario, there is no hope that we can extend such a continuous function $f$ to obtain a new continuous function $\widetilde f : \overline X \to Y$ . The following counter-example demonstrates this:

Let $X = [0,\frac 12 ) \cup (\frac 12, 1]$ and let $f$ be any continuous function on $X$ such that there is a positive gap between $f(\frac 12+)$ and $f(\frac12-)$ . For example, we can choose

$\displaystyle f(x)=\begin{cases}x^2&\text{ if } x<\frac 12,\\x^3 & \text{ if } x>\frac 12.\end{cases}$

Since $f$ is monotone increasing, we clearly have

$\displaystyle f(\frac12-)-f(\frac 12+)=\frac18.$

Hence any extension $\widetilde f$ of $f$ cannot be continuous because $\widetilde f$ will be discontinuous at $x =\frac 12$ . Thus, we have just shown that continuity is not enough. For this reason, we require $f$ to be uniformly continuous.

SIMPLE OBSERVATIONS . We start with the following basic results.

Claim 1. Let $f : E \subset X \to Y$ be uniformly continuous. Then if $(x_n)_n$ is a Cauchy sequence in $E$ , then $(f(x_n))_n$ is a Cauchy sequence in $Y$ .

This is a very classical and simple result. The proof simply makes use of the definition of uniform continuity and Cauchy's sequence. It is interesting to note that if $E$ is closed, then we can drop "uniformly". This is because continuous function on a bounded set is always uniformly continuous.

In reverse, the statement is also true under certain conditions, for example, any real-valued function from a bounded set $E$ is uniformly continuous if it sends any Cauchy sequence to a Cauchy sequence. It is worth noting that the boundedness is essential. We do not consider the situation of functions between metric spaces in this post.

Claim 2. Assume that the hypotheses of Claim 1 hold. Then if both $(x_n)$ and $(x'_n)_n$ converge to $x$ , then

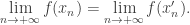
$\displaystyle \lim_{n \to +\infty} f(x_n) = \lim_{n \to +\infty} f(x'_n).$

This is also a classical and simple result. The proof goes as follows: we mix the two sequences: $x_1, x'_1, x_2, x'_2,...$ which also converges to $x$ . From this the two limits $\lim_{n \to +\infty} f(x_n)$ and $\lim_{n \to +\infty} f(x'_n)$ must be equal.

UNIFORMLY CONTINUOUS EXTENSION . Since continuity of $f$ is not enough, in general, to extend, we are forced to assume a uniform continuity. We hope that this is enough to prove that the extended function $\widetilde f$ is continuous. However, we can do more. The following claim confirms that the extended function, in fact, is also uniformly continuous.

Claim 3. Let $Y$ be complete and $f : E \subset X \to Y$ is uniformly continuous. Then there exists a unique continuous extension $\widetilde f : \overline E \subset X \to Y$ . Moreover, $\widetilde f$ is also uniformly continuous.

Proof. The proof of Claim 3 goes as follows. Let $x \in \overline E$ be arbitrary. Then there exists a sequence $(x_n) \subset E$ converging to $x$ , namely, $d_X(x_n,x) \to 0$ as $n \to +\infty$ . Clearly, $(x_n)$ is a Cauchy sequence in $E$ , which by Claim 1, implies that $f(x_n)$ is Cauchy in $Y$ . Therefore, we can define

$\displaystyle \widetilde f(x):= \lim_{n \to +\infty} f(x_n).$

The preceding limit exists because $Y$ is complete. By Claim 2, the value $\widetilde f(x)$ is independent of the choice of $(x_n) \subset E$ .

Continuity of $\widetilde f$ . We now claim that $\widetilde f$ is continuous. Indeed, fix a point $x \in \overline E$ and assume that $(x_n) \subset \overline E$ converges to $x$ . It suffices to show that

$\displaystyle \lim_{n \to +\infty} \widetilde f(x_n)= \widetilde f(x).$

To see this, given $\varepsilon > 0$ , there is $N$ such that

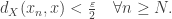
$d_X(x_n, x)< \frac \varepsilon 2 \quad \forall n \geq N.$

For each $x_n$ with $n \geq N$ , let $(x_{n,m})_m \subset E$ be a sequence converging to $x_n$ . One one hand, by the definition of $\widetilde f$ , there holds

$\displaystyle \widetilde f(x_n) = \lim_{m \to +\infty} f(x_{n,m}).$

On the other hand, given $\varepsilon > 0$ , by Claim 1, there is some $M_n$ such that

$\displaystyle d_X(x_{n,m}, x_n)< \frac \varepsilon 2, \quad d_Y(f(x_{n,m}), f(x_n))< \frac \varepsilon 2, \quad \forall m \geq M_n,$

which, by triangle inequality, gives

$\displaystyle d_X(x_{n,m}, x) \leq d_X(x_{n,m}, x_n) + d_X(x , x_n) < \varepsilon \quad \forall m \geq M_n.$

Hence

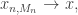
$\displaystyle x_{n,M_n} \to x,$

which implies that

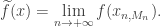
$\displaystyle \widetilde f(x) = \lim_{n \to +\infty} f(x_{n,M_n}).$

This tells us that

$\displaystyle d_Y(f(x_{n,M_n}), \widetilde f(x)) < \frac \varepsilon 2 \quad \forall n \gg 1.$

However, from the choice of $x_{n,M_n}$ , we can also estimate

$\displaystyle d_Y(f(x_{n,M_n}), \widetilde f(x_n)) < \frac \varepsilon 2.$

Hence,

$\displaystyle d_Y(\widetilde f(x_n), \widetilde f(x)) \leq d_Y(\widetilde f(x_n), f(x_{n,M_n})) + d_Y(f(x_{n,M_n}), \widetilde f(x)) < \varepsilon \quad \forall n \gg 1.$

Thus we have shown that

$\displaystyle \widetilde f(x) = \lim_{n \to +\infty} \widetilde f(x_n).$

The conclusion follows.

Uniqueness of $\widetilde f$ . This is obvious because $E$ is dense in $\overline E$ .

Uniform continuity of $\widetilde f$ . Let $\varepsilon > 0$ be given and let $\delta>0$ be such that

$\displaystyle d_Y( f(u), f(v))< \frac \varepsilon 2$

whenever $d_X(u,v)<4\delta$ . Let $x, y \in \overline E$ be arbitrary such that

$\displaystyle d_X(x, y)<\delta.$

By definition, there are two points $x', y' \in E$ such that

$\displaystyle d_X(x, x') < \delta, \quad d_Y(\widetilde f(x), f(x')) < \frac \varepsilon 2, \quad d_X(y, y') < \delta, \quad \displaystyle d_Y(\widetilde f(y), f(y')) < \frac \varepsilon 2.$

Notice that

$\displaystyle d_X(x', y') \leq d_X(x, x')+d_X(x, y)+d_X(y, y') < 4\delta.$

Hence

$\displaystyle d_Y(\widetilde f(x), \widetilde f(y)) \leq d_Y(\widetilde f(x), f(x'))+d_Y(f(x'), f(y'))+d_Y(\widetilde f(y), f(y') <\varepsilon,$

proving the uniform continuity of $\widetilde f$ .

UNIFORMLY EQUI-CONTINUOUS EXTENSION . We now turn out attention to a family of uniformly continuous functions.

Claim 4. Let $Y$ be complete and $\mathcal F$ is a family of uniformly continuous functions $f: E \subset X \to Y$ . If the family $\mathcal F$ is uniformly equi-continuous on $E$ , then the uniquely extended family $\widetilde{\mathcal F}$ of uniformly continuous functions on $\overline E$ obtained from Claim 3 is also uniformly equi-continuous.

Proof. Clearly, the unique family $\widetilde{\mathcal F}$ consists of uniformly continuous functions on $\overline E$ . We need to verify the uniformly equip-continuity of the family. By the definition, it suffices to show that given any $\varepsilon >0$ , there is some $\delta > 0$ depending only on $\varepsilon$ such that

$\displaystyle d_Y(\widetilde f(x), \widetilde f(y)) < \varepsilon$

for any $\widetilde f \in\widetilde{\mathcal F}$ and for any $x, y \in \overline E$ with

$d_X(x,y) < \delta.$

Keep in mind that the family $\mathcal F$ is already uniformly equi-continuous on $E$ . Using this fact, let $\delta>0$ be such that

$\displaystyle d_Y( f(u), f(v))< \frac \varepsilon 2, \quad \forall f \in \mathcal F$

whenever

$d_X(u,v)<4\delta.$

Now we let $x, y \in \overline E$ be arbitrary such that

$\displaystyle d_X(x, y)<\delta.$

As before, for an arbitrary but fixed function $f \in \mathcal F$ , there are two points $x'_f, y'_f \in E$ such that

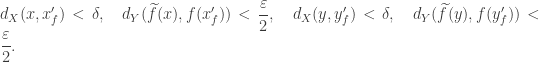
$\displaystyle d_X(x, x'_f) < \delta, \quad d_Y(\widetilde f(x), f(x'_f)) < \frac \varepsilon 2, \quad d_X(y, y'_f) < \delta, \quad \displaystyle d_Y(\widetilde f(y), f(y'_f)) < \frac \varepsilon 2.$

We use the sub index $\square_f$ to denote the dependence on the function $f$ being consider. Notice that

$\displaystyle d_X(x'_f, y'_f) \leq d_X(x, x'_f)+d_X(x, y)+d_X(y, y'_f) < 4\delta,$

which then implies that

$\displaystyle d_Y( f(x'_f), f(y'_f))< \frac \varepsilon 2.$

Putting all estimates above together we deduce that

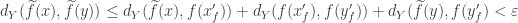
$\displaystyle d_Y(\widetilde f(x), \widetilde f(y)) \leq d_Y(\widetilde f(x), f(x'_f))+d_Y(f(x'_f), f(y'_f))+d_Y(\widetilde f(y), f(y'_f) <\varepsilon$

for any $f \in \mathcal F$ , whenever

$\displaystyle d_X(x, y)<\delta,$

proving the uniform equi-continuity of $\widetilde f$ .

AN APPLICATION . To conclude the note, we consider the well-known Arzelà-Ascoli theorem which states that any pointwise bounded sequence of functions in $C(K)$ , where $K$ is compact, which is also uniformly equi-continous, is precompact in $C(K)$ . There are counter-examples in the literature saying that the compactness of $K$ is essential. For example, any translation of a smoothly compactly supported function on $\mathbb R$ would work. We shall, however, demonstrate that we cannot construct any similar counter-example on bounded sets which are not closed.

Since the Arzelà-Ascoli theorem concerns the pointwise boundedness, in the following claim, we address this property through the extending process as before.

Claim 5. Let $Y$ be complete and $\mathcal F$ is a family of uniformly equi-continuous functions $f: E \subset X \to Y$ . If the family $\mathcal F$ is pointwise bounded on $E$ , then the uniquely extended family $\widetilde{\mathcal F}$ obtained from Claim 3 is also pointwise bounded on $\overline E$ .

Proof. Let $x \in \overline E$ be arbitrary. By definition, we need to prove that

$\displaystyle \sup_{\widetilde f \in \widetilde{\mathcal F}} |\widetilde f(x)|< C(x) <+\infty.$

Fix any $\varepsilon > 0$ and by the uniform equi-continuity of $\widetilde{\mathcal F}$ , we can let $\delta>0$ be such that

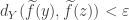
$\displaystyle d_Y(\widetilde f(y), \widetilde f(z)) < \varepsilon$

whenever $y, z \in \overline E$ with

$\displaystyle d_X(y, z)<\delta.$

By way of contradiction, there is a sequence of $\widetilde f_n \in \widetilde{\mathcal F}$ such that

$\displaystyle \lim_{n \to +\infty} |\widetilde f_n(x)|= +\infty.$

Now we choose some $y \in E$ in such a way that $d_X(x,y)<\delta$ and fix it. Clearly,

$\displaystyle |\widetilde f_n(x)| \leq |\widetilde f_n(x)-\widetilde f_n(y)|+|\widetilde f_n(y)|< \varepsilon +\sup_{\widetilde f \in \widetilde{\mathcal F}} |\widetilde f(y)|.$

Since the right hand side is bounded, we obtain a contradiction. Hence the extended family $\widetilde{\mathcal F}$ is also pointwise bounded.

Combining Claims 4 and 5 we deduce that on any pre-compact subset $K$ , a family of functions in $C(K)$ which is also pointwise bounded and uniformly equiv-continuous is pre-compact in $C(K)$ . Therefore, we are in position to conclude that one cannot construct a counter-example of the well-known Arzelà-Ascoli theorem against the compactness of $K$ , however, only on any bounded subset $K \subset \mathbb R$ . An unbounded set is the only possibility that we can construct.

I thank Nguyễn Đức Bảo for useful discussion during the preparation of this note.

jimenezentrught.blogspot.com

Source: https://anhngq.wordpress.com/2019/04/14/extending-functions-between-metric-spaces-continuity-uniform-continuity-and-uniform-equicontinuity/

Suppose That the Function F a b r is Uniformly Continuous Prove That F a b r is Bounded

0 Response to "Suppose That the Function F a b r is Uniformly Continuous Prove That F a b r is Bounded"

Enregistrer un commentaire

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel